WAVELET BASED IMAGE COMPRESSION SYSTEM

Project Supervisor Masood Ahmad Assistant Professor Department of Electrical Engineering University of engineering & Technology, Lahore Pakistan Project Team Members Hamid Rahim Sheikh (Team Leader) Aamer Munir
The general method of achieving Transform Based Image Compression is shown in Figure 1. The input image is transformed into a different domain using one of the many available Linear Transforms and then quantized. The quantized transform coefficients are coded loss-lessly & stored/transmitted. The reciever decodes the coefficients and recontructs the image by applying the Inverse Transformation. The output is distorted by the Quantization Noise introduced in the signal in the quantization step. The magnitude of the distortion is directly related to the compression ratio given to the bit allocator via the Rate Constraint.

Figure 1: Block Diagram of Image Compression System

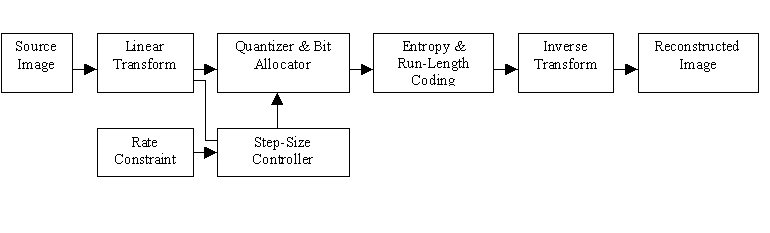
We used a Discrete Wavelet Transform Based method to achieve Image Compression. In this scheme, the 2-D Discrete Wavelet Transform of the image is obtained by passing the image through a Perfect Reconstruction Filter Bank. The filters comprising the bank are 2-D FIR filters with specialized coefficients for which the conditions of Perfect Reconstruction, Convergence & Stability of Basis Functions hold true. The Filter Bank outputs different subbands of the image which constitute the 2-D DWT of the image.

For our implementation, we tried different factorizations of the Maxflat (Daubechies) polynomial [Strang]. We tested Biorthogonal 9/7, 6/10 & 7/17 factorizations but found the 9/7 to be the most superior in terms of perceptual quality. The 2-D 9/7 system was constructed from the 1-D prototypes, and thus our implementation uses a Separable construction. The 2-D 9/7 Basis Functions for Decomposition & Reconstruction show symmetry in horizontal & vertical directions only.

For quantization, we used an optimal Bit Allocation algorithm based on the Rate Distortion Theory (as outlined by [Strang]). The Bit Allocation Algorithm uses the variances of the subbands together with their perceptual weight and relative subband size to determine an optimal bit allocation which satisfies the output Rate Constraint supplied by the user.

For the loss-less source coding step, we used Run-Length & LZ coding. We used GZIP (unix utility) for the LZ compression step. We found that Run-Length coding was a rather redundant step and lead to insignificant improvements in the bit rate. Simple LZ coding of quantized coefficients was about as good as the combination of Run Length & LZ.

At the reconstruction side, the synthesis bank assembles the reconstructed image from the quantized transform coefficients.

For our implementation, we used C++ in Linux environment. Our Code allows not only simple octave band Filter Banks, but the Filters can be 'wired' into other possible configurations as well.

We tested the algorithm for different wavelets, and at different Bit Rates. The results show a definitive improvement over the JPEG standard. Our implementation uses a simple source coding method (GZIP) but better methods like those based on Zero Trees can give superior results [Amir].